As it is usual when comparing capability in completing intelligence tasks by man against machines, we notice that people can effortlessly categorise basic spatial relationships between objects that are useful in performing tasks like reasoning and planning, or in engaging in a conversational activity to reach a goal. The objects may be at a distance from the observer, and even the objects themselves may be at a long distance from each other. In any possible setting, we may want to know how two objects relate together in terms of a fixed set of spatial relationships that are commonly used in people’s daily life.
Computationally, we may need to know these relationships by being given only a colour photograph of some objects and rectangular boxes covering all of the objects of our interest. For example, given that input, we may want to state that “one object is below another object” — or, in another case, we would want to say that “object A is to the left of object B, and object A is behind object B”. We immediately deduce that spatial correspondences relating pairs of objects can simultaneously admit at least one relationship.
Open-sourcing AI software
In the domain of Artificial Intelligence (AI), an algorithm to infer the spatial relationships between objects (by usually considering objects in pairs) could be useful if it was implemented and shared with developers around the world as a library routine that any AI developer would want to have in place. In about the last fifteen years, we have globally seen a trending practice of sharing code with the public as open-source code. Code implementing very important algorithms or intelligent workflow processes is shared with any developer, provided that they acknowledge the terms of a license agreement like the GPL, L-GPL or the MIT license. Then, the need for developers to reimplement the wheel for basic tasks becomes smaller and smaller as code gets continuously contributed publicly, by offering to them robust implementations of algorithms for different intelligent tasks and for a row of programming languages. If there is still something that a developer cannot find in an open-source software library that is dedicated to a specific domain of problems (for example, computer vision problems), they can dig into the available code and extend it for themselves to fit their technical requirements. If their contribution of features is important and useful for other programmers who may be in need of the same features, they can commit their code changes to the maintainers of the software library (or any other open source-type software) for review. Hopefully, their contribution will be included in a future release of the software.
Capturing failures
Software engineers developing robotics applications, for example, would have wanted to have a set of such routines to use in developing simulation workflows for robots interacting with objects. About the one side of the coin, these routines should be reliable enough to be reused in software applications that feature sufficiently correct error handling and some ability to leverage failure evidence generated by the model. These are useful in order to achieve correctness and better error control in an underlying application.
What AI programs “see”
Although humans can reason effortlessly and very accurately in terms of basic spatial relationships that relate pairs of objects, this task is not as easy to be solved by computers. While humans can, for instance, see two objects and state that “the blue car is next to the lorry”, computers instead are only given a rectangular table of numbers that define the red, green and blue colour intensities of the cells in the table. These cells in this table correspond to the pixels of the underlying colour image. Although, again, humans can sense objects visually and understand spatial relationships instantly, we can instead state that computers are only initially given this table of colour pixel intensities. Then the goal is to use a program that takes in this rectangular array of pixel intensities and bounding boxes covering two objects of interest, and the program should decide how the two objects inside the two bounding boxes relate spatially. The program acts like an “artificial brain” specifically targeted to solve only this task and nothing else, that can understand the table of numbers that was input. It is helpful to realise that the program that does this operation executes a sequence of steps that finally yield a decision about the input that is given to the program. This is a basic realisation that is taught in introductory programming courses: that programs implement algorithms and that programs implementing algorithms need to receive input data and produce output data.
Usefulness of spatial relation prediction
The steps implemented in a program that identifies the spatial relationships between two objects in an image, were first devised by an algorithm that was designed to take in said input describing two objects in an image and produce as output the actual spatial relation out of a set of relations. At any given point in time, the program may be correct about the output it produces, or it may commit a wrong answer. Having such a program being correct at 100% of the time seems impossible at the moment, but it could be possible in future advances. It is important to note that this output may be reported to the person operating the computer, or the output can be passed on to another computer program that considers this output relation and then makes other decisions. For example, we may want to have a computer program that can execute a particular operation provided that one or more conditions hold. For instance, in a monitoring application that receives data from a camera, one case of a conditional execution that considers the spatial relationships between two detected entities (objects) could be this: “if a (detected) person is on the (detected) staircase, then turn the light on”.
Notice that by being able to correctly control that “a (detected) person is on the (detected) staircase”, developers can completely bypass the necessity to write complicated geometric or algebraic rules of what it means for one object to be on another object. This can be a potential failure point in the development process that is hard to cross safely without getting into trouble, as developing such rules may be wrong for some inputs and may work okay for other inputs. As a downside, a machine learning algorithm for this task would also make errors and the application logic of our program would want to “know” why. Fortunately, advances in all the settings met here so far, can enable us to write applications that reason about the spatial relationships of objects in colour images.
RelatiViT: a state-of-the-art model

It is important to note that computer algorithms are still not excellent at deciding the spatial relationships between objects (we refer only to pairs of objects). In a recent paper presented by Wen and collaborators [1] at the ICLR 2024 in Vienna, the authors devised modern spatial relationship classification algorithms that are based on deep convolutional neural networks or on Transformer [2] deep neural networks. The authors distinguished one of the models that they designed, called RelatiViT, as a superior model identified by conducting comparative experiments in two benchmarks. This computer vision algorithm can decide how two objects relate spatially when it is given a colour photograph of the objects with a surrounding background, along with rectangular bounding boxes covering the two objects.
Wen et al. used two benchmark datasets with examples of objects and bounding boxes covering them (see Figure 1); some portion of the data was reserved to train their spatial relationship classifier, and another portion of it was used to see how well their algorithm could generalise on that yet unseen data. This is a standard practice when building a machine learning model. We want to evaluate how good the model is empirically. Note that having a model being evaluated on at least one example that was used to train the model is unwanted. However, we can do that if we wish outside model testing. The first benchmark provided pairs of objects in 30 spatial relationships, and the second benchmark provided 9 spatial relationships. Interestingly, the 9 spatial object relationships that one of the benchmarks considers are: “above”, “behind”, “in”, “in front of”, “next to”, “on”, “to the left of”, “to the right of” and “under”.
Quantitative score of success
For the two benchmarks, the authors reported that the average ratio of correct spatial relationship classification with respect to each spatial relationship is a little higher than 80%. This essentially means that, in the controlled benchmark, the RelatiViT model can on average respond correctly to 8 out of 10 inputs respective of the actual spatial relationship that is picked and provided that all of the available test cases in the benchmark are tried.
Adoption of advances circa ‘17
In the last seven years, a basic and thriving technique in general-purpose deep learning algorithms has been the design of a machine learning model called the Transformer. This model was proposed in 2017 by Vaswani and collaborators [2], and it has been cited more than 139.000 times at the time this article was written. The Transformer model is an advance in deep learning that researchers have been putting effort to study, reuse or redesign in formulations of different sorts for machine learning problems. One important conclusion that is essential to accept a new machine learning model as a successor model (or winning model) for a particular problem, is that the models employing formulations that involve a Transformer-like model are empirically better than models that employed previous regimes of basic models or algorithms (such as, for instance, Generative Adversarial Networks or other past developments). Superiority is always measured in terms of one or more quantitative metrics, although this essential practice has received constructive criticism by researchers in recent years. At this point, there is a puddle in the road which is good to know: accepting that, for instance, Transformers are successful successor models against previous theory does not devalue previous theory. It certainly, however, implies that a better solution could exist by reusing the recent advance according to a row of quantitative metrics (which are still not the end of the story when we compare a sequence of models together in terms of their merits).
Basic input/output in a Transformer
The basic operation performed by a Transformer model is receiving as input a list of vectors and outputting a list of corresponding vectors by first identifying/capturing the true associations between the vectors in the input list. This model is being used in a very large set of basic AI problems. For instance, some of the important applications or application areas are: image segmentation, classification problems of all sorts, speech separation problems, or problems regarding the remote sensing of Earth observation data. Researchers have been committing time and effort to formulate virtually all known basic machine learning problems (like classification, clustering, etc.) reusing the idea of the Transformer model by Vaswani et. al. [2].
Structure of the RelatiViT
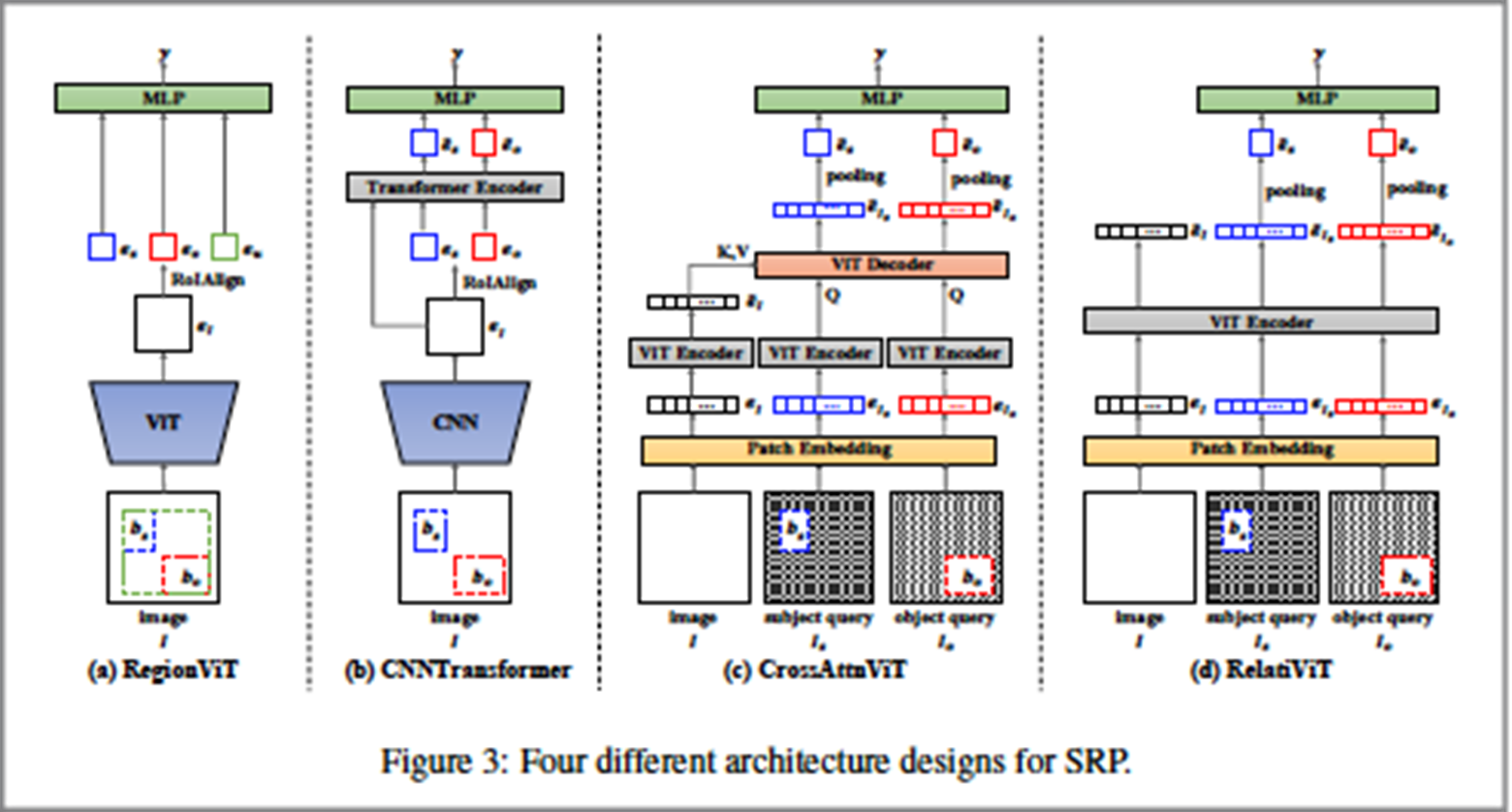
Wen et al. [1] considered four models (see Figure 2) that can take as input a colour image and two bounding boxes covering two objects of a user’s interest. In this article, we only focus on the rightmost model: the one called RelatiViT. RelatiViT is a state-of-the-art model that not only encodes information about two objects, but it also encodes information describing the context of the image. People certainly employ such cues in their decisions. The context of the image is regarded as the clipped portion of the image background that is enclosed by the union of the bounding boxes covering two objects: the subject and the object. For an example of what context is, see Figure 2 (a). Obviously, the information (or even the raw data) related to the surround of two objects is very important in deducing how two objects in a colour image are arranged spatially.
The RelatiViT model processes data in five basic steps: (a) it initially considers small image patches that reside in the background of the image, and small patches that reside in the trunks of the two objects; thereby creating three lists of patch embeddings; (b) these three lists of embeddings are passed through a ViT encoder [3]; (c) the ViT encoder recalculates (or “rewrites”) the vectors in each of the three lists so that they now are better related with each other, producing three new identical sets of embeddings; (d) since the two objects should be described by one vector each, RelatiViT considers complementary information available in a set of embeddings, and uses a pooling operation to calculate a single representation that can act as a global representation that employs features from the partial representation vectors; and finally, (e) the pooled representations of the two objects and the representations of the object context are passed to a multilayer Perceptron model (MLP) that can decide the spatial relationship characterising the two objects. Therefore, the MLP model learns how to map object-specific features to spatial relationship classes when RelatiViT is trained on example triplets (of a subject, an object and a ground truth spatial relationship relating the subject and the object), and it learns such a mapping by being provided small batches of data containing object-pair features and associated spatial relationships. To train RelatiViT, we may need at least one modern GPU that can be mounted on a regular modern personal computer with enough RAM memory capacity. Software stacks such as PyTorch and tensorflow have been implemented in the last decade, allowing machine learning and computer vision developers to design prototypes of deep neural netwoks and train them on data.
Generating explanations
Before we conclude this article, here is an important question which will always reappear when developing machine learning models in general: Can we reuse models like RelatiViT for any critical application where errors could be harmful or intolerable? We should first recognise that developments like the RelatiViT, only target to create models that can be good classifiers to recognise spatial relationships between objects. They propose models that are crafted by making use of the designer’s understanding of how such a model should be designed and no further features like classification validation are sought. One could quickly believe that this is a flaw of the method, but it is not. Each piece of research has to plan a scope so that only contributions within that scope can be committed in the research work. However, how to prove (if applicable) why a decided spatial relationship is in fact the true relationship connecting two objects falls within the subject of explainability in the deep learning field. Explainability models uncover and report evidence about a particular decision, and they are relevant for almost all of the basic machine learning problems (including, for instance, classification and clustering). For instance, if “object A is to the left of object B”, then this is the case because the mass of the second object is situated to the right of the mass of object A. However, another explanation for that could be that the center of mass of the two objects are ordered in this way, and we can deduce that by only comparing the magnitude of the projections of the centres of mass of the two objects across the horizontal axis. By doing so, we can then calculate the relative spatial relationship between two objects. We start to realise, then, that there can be many explanations that describe the same event. Some explanations are identical, but they are stated (or expressed) alternatively. Other explanations are complementary, and are useful to be reported to the user of a spatial relationship classifier. An explanatory model in a deep learning system such as the one that this article regards, should provide to the user as much comprehensive evidence as possible, and as many pieces of evidence as the explanatory algorithm can provide thanks to its design. But here is another important thing that is very critical by nature: can we just trust explanations and think of them as being correct without reasoning further about their correctness? The answer to this question is no, unless the algorithm can provably produce explanations that can be verified before it reports them to the user. This can become possible when we are limited to a particular application out of the very large pool of possible machine learning problems and data.
References

Sotiris Karavarsamis
Research Assistant at Visual Computing Lab (VCL)@CERTH/ITI
&

Petros Drakoulis
Research Associate, Project Manager & Software Develper at Visual Computing Lab (VCL)@CERTH/ITI





